Zarankiewicz Algorithm 1: Pruning the Search Tree
This post is the fourth in a series of posts about my computational approach to the Zarankiewicz problem.
So far we have a rudimentary backtracking algorithm which beats brute force, but not much else. However, it's still embarrassingly easy to improve: the algorithm wastes a lot of time investigating partial solutions which
- Are unlikely to lead to an optimal solution, meaning we should try them later when we have a better lower bound on the solution;
- Cannot lead to an optimal solution, meaning we should just reject them immediately; or
- Are symmetric to other partial solutions we considered earlier, so they can't lead to a better solution than one we already found. We can reject these too.
That means there are large branches of the search tree which we're exploring unnecessarily. We want to prune these branches; let's consider our options.
Number 1 is the order we navigate the search tree in. At first glance, this seems irrelevant: visiting the same nodes in any order should take the same total time. However, once we notice that finding a solution quickly gives us a lower bound which can be matched against an upper bound, we realise that the order does matter, because we might end up visiting fewer nodes.
Considering the rows as binary numbers, we're trying from $00000$ to $11111$ by incrementing. This means we're first trying rows without many $1$s; but we want as many $1$s as possible. Perhaps we should start at $11111$ and decrement; on the other hand, putting a lot of $1$s into the first row right away will severely constrain how many $1$s we can fit in the remaining rows, since there will be many more potential rectangles to be avoided.
These options are mutually exclusive; we can only pick one order to navigate the tree in, so we'll want to compare which option is best.
Number 2 is how we reject partial grids. If the upper bound on the potential weight of a partial grid is less than the lower bound on the optimal solution, then the partial grid can be rejected. The lower bound is given by whatever solution we've already found, so what we need is upper bounds. A simple way to bound the weight of a potential solution would be to total the weights of the filled rows, and add $n$ (the number of columns) per unfilled row. We'll call this the naïve bound, and it works for the trivial reason that a row can't have more $1$s than it has columns.
There are other ways to get an upper bound, and they're complementary; we can compute as many as we want, and having more probably allows us to prune more of the tree. We don't need to choose one "best" method.
In "post 0" of this series, we counted pairs of columns to get an upper bound. Let's revisit that argument in the context of our backtracking search algorithm, where grids have some rows already filled in:
| $\begin{pmatrix} 0 & \bbox[2pt,#FF8080]{1} & \bbox[2pt,#FF8080]{1} & 1 \\ 1 & \bbox[2pt,#80FF80]{0} & \bbox[2pt,#80FF80]{0} & 1 \\ * & \bbox[2pt,#80FF80]{*} & \bbox[2pt,#80FF80]{*} & * \\ * & \bbox[2pt,#80FF80]{*} & \bbox[2pt,#80FF80]{*} & * \end{pmatrix}$ | $\begin{pmatrix} 0 & \bbox[2pt,#FF8080]{1} & 1 & \bbox[2pt,#FF8080]{1} \\ 1 & \bbox[2pt,#80FF80]{0} & 0 & \bbox[2pt,#80FF80]{1} \\ * & \bbox[2pt,#80FF80]{*} & * & \bbox[2pt,#80FF80]{*} \\ * & \bbox[2pt,#80FF80]{*} & * & \bbox[2pt,#80FF80]{*} \end{pmatrix}$ |
| $\begin{pmatrix} 0 & 1 & \bbox[2pt,#FF8080]{1} & \bbox[2pt,#FF8080]{1} \\ 1 & 0 & \bbox[2pt,#80FF80]{0} & \bbox[2pt,#80FF80]{1} \\ * & * & \bbox[2pt,#80FF80]{*} & \bbox[2pt,#80FF80]{*} \\ * & * & \bbox[2pt,#80FF80]{*} & \bbox[2pt,#80FF80]{*} \end{pmatrix}$ | $\begin{pmatrix} \bbox[2pt,#80FF80]{0} & 1 & 1 & \bbox[2pt,#80FF80]{1} \\ \bbox[2pt,#FF8080]{1} & 0 & 0 & \bbox[2pt,#FF8080]{1} \\ \bbox[2pt,#80FF80]{*} & * &* & \bbox[2pt,#80FF80]{*} \\ \bbox[2pt,#80FF80]{*} & * &* & \bbox[2pt,#80FF80]{*} \end{pmatrix}$ |
For each highlighted pair of columns, adding a row with $1$s in both columns would create a rectangle. In effect, each completed row "claims" some pairs of columns, forbidding rows below it to have $1$s in both. Importantly, the number of pairs claimed by a row is only determined by its weight, not where the $1$s are: if a row has weight $w$, it claims ${w \choose 2} = \frac{1}{2}w(w-1)$ pairs of columns. In this example, the first row claims three pairs and the second row claims only one.
Since there are only finitely many pairs of columns in total, only finitely many pairs remain to be claimed by the rows yet to be filled in. If the number of unclaimed pairs is $T$, the remaining rows must have weights $w_i$ satisfying $\sum \frac{1}{2}w_i(w_i-1) \le T$, putting an upper bound on $\sum w_i$ and hence on the weight of a completion. We'll call this the convex optimisation bound, because as we identified earlier, maximising $\sum w_i$ in this expression is a convex optimisation problem.*
Number 3 is called symmetry reduction. Permuting the rows and columns of a grid preserves its weight and the rectangle-free property, so there are many optimal solutions, and we only need to find one. To take advantage of this, we can search only for grids in a particular form, and ignore any partial grids not in that form; this is valid if symmetries guarantee at least one optimal grid in that form.
It's not yet obvious what demands we can make about the form of the solution, but a simple one is requiring the rows to be in order. It's easy to guarantee there is an optimal solution with its rows in order, and this is intuitive when you think about the kinds of solution that our algorithm already finds:
$$\begin{pmatrix} \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & 1 & 1 \\ \cdot & \cdot & \cdot & \cdot & 1 & 1 & \cdot & 1 \\ \cdot & \cdot & \cdot & 1 & \cdot & 1 & 1 & \cdot \\ \cdot & \cdot & 1 & \cdot & 1 & \cdot & 1 & \cdot \\ \cdot & 1 & \cdot & 1 & 1 & \cdot & \cdot & \cdot \\ \cdot & 1 & 1 & \cdot & \cdot & 1 & \cdot & \cdot \\ 1 & \cdot & 1 & 1 & \cdot & \cdot & \cdot & 1 \\ 1 & 1 & \cdot & \cdot & \cdot & \cdot & 1 & \cdot \end{pmatrix}$$
(I've replaced each $0$ with a $\cdot$ to make this easier to see.) There are $8! = 40{,}320$ solutions with these same rows in various orders, but this is the first one the plain backtracking algorithm found, and its rows are in order (as binary numbers), even though we didn't ask for them to be! This is no coincidence: grids with their rows in order appear earlier in the search tree than their symmetric counterparts, so of course we find them first. The issue is that we don't then need to find the other $40{,}319$ permutations.**
We could implement symmetry reduction by making the rejectNode() method reject out-of-order rows. However, this is wasted effort; if the current row is $01001$, for example, then we know we're going to reject any new row earlier than $01001$; why even try them? We could simply skip over these nodes when we're navigating the tree: instead of starting new rows at $00000$, we can make the descend() method copy the state of the current row.*** Let's call this strategy lexicographic order, or lex order for short, because the rows are in "alphabetical order" as strings. (This is only true because we used the "increment" strategy; if we decrement instead, it will still be "alphabetical order" in a sense, but our "alphabet" will have $1$ before $0$.)
Different symmetry reduction rules may be complementary or mutually exclusive, depending on what they are. This is going to be the main source of complexity in the algorithm we're working towards; we might have $20$ different demands, and we'll need a way to decide whether they can all be demanded simultaneously.
There are three dimensions of variation - the order we navigate the tree, the choice of upper bounds, and whether we use symmetry reduction - so there are many combinations to compare. To keep it manageable, let's not compare options where we know what will be faster:
- Symmetry reduction is free, since we're skipping nodes rather than adding extra checks (which would take CPU-time).
- The convex optimisation bound will reject all of the same nodes as the naïve bound, and more: the naïve bound says an unfilled row might be full of $1$s, whereas the convex optimisation bound says that would claim every pair of columns. The naïve bound should be faster to compute, so we'll still try it, but there's no need to use both at once.
To enable such varied combinations of strategies in our code, a Solver has a Navigator and a list of Rejectors, where the Navigator is responsible for defining the descend(), canAdvance(), advance() and ascend() methods which navigate the search tree, and each Rejector defines a rejectNode() method. (A Bound is a kind of Rejector.)
Enough talk; let's see the results:
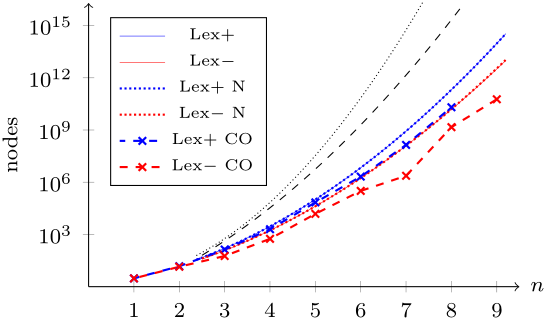
$+$/$-$: increment/decrement, N: naïve bound, CO: convex optimisation bound.
Some observations:
- Lex order makes a huge improvement: all of these options beat plain backtracking, by an even bigger margin than backtracking beats brute force.
- Decrementing and the convex optimisation bound are the clear winner; both are improvements by orders of magnitude. They complement each other well, because the convex optimisation bound is good at rejecting the early rows that have too many $1$s, so we get to the right number of $1$s fairly quickly.
- The naïve bound is useless; it rejected so few nodes that you can't see the difference on the graph. Going by running time, the algorithm was actually faster without it, because computing the bound isn't free.
- For some sizes like $7{\times}7$ and $9{\times}9$, BT lex$-$ CO gets lucky, and finishes sooner than a best-fit curve would predict. This doesn't happen for either BT lex$+$ CO or BT lex$-$, so it's probably because the convex optimisation bound does much more work when it can be matched against a good lower bound, and lex$-$ sometimes sporadically finds the optimal solution faster than usual, whereas lex$+$ consistently wastes time trying empty rows before it gets to the solution.
From here on we'll forget about lex$+$, and just refer to lex$-$ as lex. This implies our "alphabet" has $1$ before $0$, so to avoid cognitive dissonance we'll stop writing the $0$s.
Let's go further. To improve on this strategy, we might learn something from the kind of solutions it finds:
$$\begin{pmatrix} 1 & 1 & 1 & 1 & \cdot & \cdot & \cdot & \cdot \\ 1 & \cdot & \cdot & \cdot & 1 & 1 & \cdot & \cdot \\ 1 & \cdot & \cdot & \cdot & \cdot & \cdot & 1 & 1 \\ \cdot & 1 & \cdot & \cdot & 1 & \cdot & 1 & \cdot \\ \cdot & 1 & \cdot & \cdot & \cdot & 1 & \cdot & 1 \\ \cdot & \cdot & 1 & \cdot & 1 & \cdot & \cdot & 1 \\ \cdot & \cdot & 1 & \cdot & \cdot & 1 & 1 & \cdot \\ \cdot & \cdot & \cdot & 1 & 1 & \cdot & \cdot & \cdot \end{pmatrix}$$
If you have a keen eye, you'll notice that not only are the rows in lex order, they're also in descending weight order; and the columns are in lex order too. Is this a coincidence, or can we make all three demands?
Proposition. The following grid has no symmetric counterpart whose rows are in both lex order and descending weight order:
$$\begin{pmatrix} 1 & 1 & 1 & 1 & \cdot & \cdot & \cdot & \cdot \\ 1 & \cdot & \cdot & \cdot & 1 & 1 & 1 & \cdot \\ 1 & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & 1 \\ \cdot & 1 & \cdot & \cdot & 1 & \cdot & \cdot & 1 \\ \cdot & \cdot & 1 & \cdot & \cdot & 1 & \cdot & 1 \\ \cdot & \cdot & \cdot & 1 & \cdot & \cdot & 1 & 1 \end{pmatrix}$$
Proof. By exhaustion. (There are only $6! \times 8!$ counterparts to try…)
That's a "no", then: symmetry doesn't guarantee a solution meeting these two demands. However, other combinations are compatible:
Theorem. Every grid has a symmetric counterpart whose rows and columns are in lex order.****
Proof. We'll achieve this by sorting the rows, then the columns, then rows, then columns, and so on; when the grid stops changing, the rows and columns must both be in order. It remains to be shown that the grid does eventually stop changing.
Consider our algorithm with the "decrement" strategy but no symmetry reduction. As we noticed above, if we sort the rows of a grid in lex order, then this grid will be visited earlier by the algorithm.
In fact, sorting the columns results in a grid the algorithm visits earlier, too:
$$\newcommand{\zerodot}{\llap{\vphantom{1}}{\,\cdot\,}} \begin{pmatrix} 1 & \cdot & \bbox[2pt,#FF8080]{\zerodot} & \bbox[2pt,#80FF80]{\zerodot} & \cdot \\ 1 & 1 & \bbox[2pt,#FF8080]{\zerodot} & \bbox[2pt,#80FF80]{1} & \cdot \\ \cdot & 1 & \bbox[2pt,#FF8080]{1} & \bbox[2pt,#80FF80]{\zerodot} & 1 \\ & & \vdots & & \end{pmatrix}$$
Consider the first pair of columns out of order: swapping them will not affect any row with $\bbox[2pt,#FF8080]{1}~\bbox[2pt,#80FF80]{1}$ or $\bbox[2pt,#FF8080]{\zerodot}~\bbox[2pt,#80FF80]{\zerodot}$ in these two columns, so the first row affected has $\bbox[2pt,#FF8080]{\zerodot}~\bbox[2pt,#80FF80]{1}$, as in the example. (If it was $\bbox[2pt,#FF8080]{1}~\bbox[2pt,#80FF80]{\zerodot}$ then these columns would already be in lex order.) Swapping them therefore leaves this row earlier in lex order, and the rows above it unchanged; so the algorithm would visit the resulting grid earlier than the original one.
The result follows because we can't keep going earlier and earlier indefinitely. $\square$
This also explains why the solution above had its columns in lex order; that wasn't a coincidence.
Descending row weight order is compatible with column lex order, too, and the proof is almost the same: but instead of considering the "decrement" navigation strategy, the algorithm in the proof must try rows in descending weight order, and rows of equal weight in lex order. Let's call this weightlex order; it's interesting that by proving that these two demands are compatible, we get - as a byproduct - instructions for how to do it.
As before, we can simply skip nodes whose rows are out of order. Enforcing column lex order isn't free, though: we'll need another Rejector to reject grids whose columns are out of order.*****
By demanding a solution in weightlex order, we get another upper bound: the weights of the remaining rows must be less than or equal to the weight of the most recently added row. Let's call this the descending row weight bound.
We have more strategies to try! Let's try them:
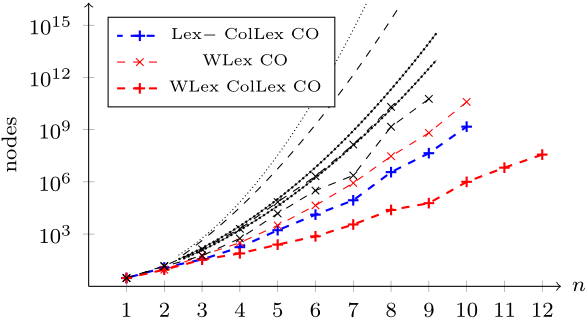
ColLex: column lex order, WLex: weightlex order and descending row weight bound.
The story continues: for all the orders of magnitude we've pruned from the search tree, lex still only gets us to $8{\times}8$, decrementing and the convex optimisation bound together get us to $9{\times}9$, weightlex gets us to $10{\times}10$, and column lex then gets us to $12{\times}12$. It's a long way to $31{\times}31$…
*By the same argument as before, the maximum of $\sum w_i$ is achieved when the $w_i$ differ by at most $1$, so this maximum can be found by a direct calculation.
**Unfortunately, this won't make the algorithm $m!$ times faster; we still have to explore some branches of the search tree which contain symmetric counterparts, because they don't only contain symmetric counterparts. In fact, an asymptotic speed-up by a factor of $O(m!)$ can never be possible, because that's higher than the complexity of the algorithm itself, which should be something like $2^{O(mn)}$, if we keep $n$ fixed.
***Although not visiting nodes is faster than visiting and rejecting them, this strategy does commit us to using the same ordering for symmetry reduction as we use for navigation; in principle, these need not be the same. We want our ordering for symmetry reduction to prune more of the tree and enable better upper bounds (as weightlex does), but this may be incompatible with the desire to find good solutions early.
****Notice that we made no mention of which alphabet the symbols in the grid come from, or the rectangle-free property of the grid. This is a very general result, so unsurprisingly it's already known; this conference paper by Flener et al. (2002) gives essentially the same proof. Interestingly, their example (on page 3) is the Zarankiewicz problem, though they don't identify it by name!
*****Actually, I did write an algorithm which gives column lex ordering for free: by grouping the columns into sections which "can still be permuted", we only need to generate rows which, within each section, have all of their $1$s on the left hand side. The first row has only one section, and each section defines one or two sections in the row below it, forming a binary tree structure. Getting it to work with weightlex is tricky, but possible, and faster; I won't explain it here, though, because it doesn't advance the narrative towards the even faster algorithms.






